The Ingenious, Glyph-Like Number System Created By Medieval Monks
Like many things, numbers are taken for granted. But imagine the small, tribal, barter-and-favor-based economy that humanity lived within for most of its existence: What need would there be to count, say, 248 medium-sized branches in exchange for 85 shucked nuts? It would never happen. In fact, as The Conversation explains, languages still exist today that don't contain specific numbers, like those of "anumeric" people such as the Munduruku and Pirahã in the Amazon rainforest. Try explaining our numerical system to them — count 1 to 9, switch to 10 and add 1 to 9, then double 10 to 20 and add another 1 to 9, etc. — and they might balk or just laugh.
So, then, imagine having to invent a number system from scratch. Start with basic numeracy and counting: What does "1" look like? "2"? How about "1,564"? Why separate numbers into multiplicative intervals of 10, 100, 1000, etc., at all? This "Arabic" number system started in India in the 5th century C.E. and made its way to Europe through the Arabic world by the 8th century C.E., per the Economic History Society. There was no universal number system by then, and plenty of time to course correct if necessary.
Enter some very clever monks of the Cistercian order circa the 13th century around the border between modern-day Belgium and France, per ZME Science. They invented a system of numbers that used one glyph-like or rune-like character to represent any number, no matter how complex — at least through 9,999.
One figure for one number
It's a little tricky to explain the Cistercian number system using words — it's made of stick-like figures, after all — but we'll do our best. The system might seem tricky, but only at first. Ultimately, it makes a heck of a lot of sense, and maybe makes for some fun cryptographic shenanigans on the side.
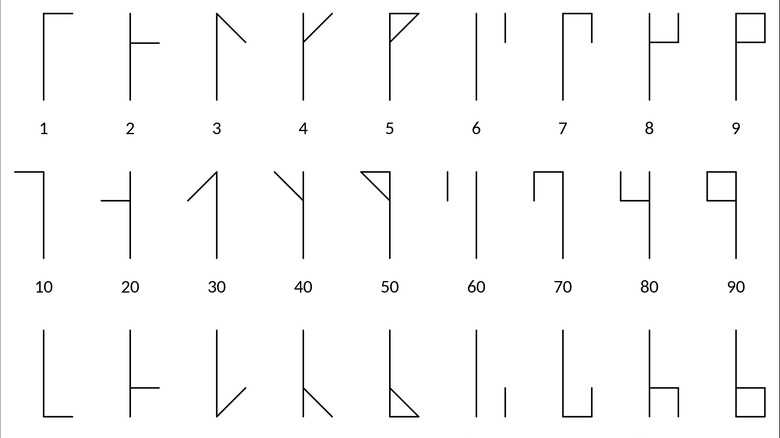
To write a Cistercian number start with a single vertical line — easy. That line will always be present no matter what number you write. Then, imagine the line bisects four quadrants that proceed in this order: upper right of the line, upper left, lower right, lower left. Upper right contains the "ones" digits: 1 through 9. Upper left contains the "tens" digits: 10, 20, 30, 40, etc. Lower right contains the "hundreds" digits: 100, 200, 300, 400, etc. Lower left contains the "thousands" digits: 1000, 2000, 3000, 4000. We're not too sure what happens when you reach 10,000 or more, but you could always just add two or more glyphs together. The system is flexible, anyway.
In each quadrant you make a little mark, and those marks are consistent by digit across all quadrants. For example: 5, 50, 500, and 5000 are little flags. Nine, 90, 900, and 9000 are boxes. Depending on the number, you make an appropriate mark in each quadrant, and bam: You've got one figure for one number, no matter how complex.
[Featured image by Meteoorkip via Wikimedia Commons | Cropped and scaled | CC BY-SA 4.0]
Good for some things, not for others
So now that you know the what and the how, how about the why? To tell the truth, it's not clear why some monks of the Cistercian persuasion took up the mantle of numeracy across the medieval Christian European world. However, as the National Catholic Register explains, we know that the system can be traced to one person: John of Basingstoke, archdeacon of Leicester — archdeacon being a decently high rank in the Church of England. Basingstoke was a scholar of ancient Greece, and the system is apparently some kind of modified ancient Greek system.
Basingstoke's number system wasn't just a small pet project, though. As the National Catholic Register says, it actually gained traction from the 13th to 15th centuries all the way from Portugal to Italy and up through Poland and Sweden. More than being used for addition, subtraction, etc., the system was used for annotations: indexing and cataloging, package deliveries, agricultural records, early hydraulic engineering markings, measuring wine barrels, and per ZME Science, notes regarding astrolabes and astronomy. However, the system wasn't great for calculations. That, combined with difficulties printing the numbers in a post-printing press age, meant that the system gave way to the Indian-Arabic system that we know and use today.
But for those curious about tinkering who want a deeper dive, sites like dCode convert standard numbers into Cistercian symbols. At the very least, you can make a semi-secret code game for you and your kids.