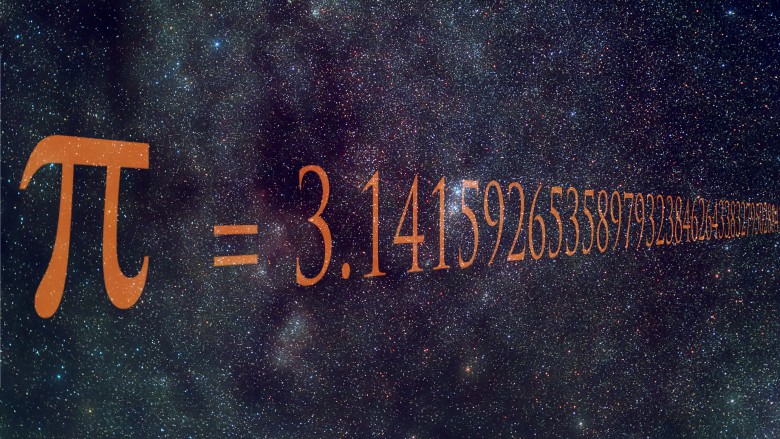Equations With Mysterious Properties
Equations aren't just lame things that we had to memorize in school. They're pretty amazing, and in some cases, they're mysterious to geniuses and laypeople alike. These are some of the coolest equations that we have stumbled upon and totally make us rethink the world we are living.
Poisson's distribution
Predicting the future would be awesome. We could find out if the Cubs will ever win a World Series again, if The Last Jedi will be any good, and how much junk mail we'll receive each day. Most future predictions are guesses or mystical mumbo-jumbo. Then there's the Poisson distribution.
Poisson's distribution lets scientists take a bunch of data, graph it, and predict future events based off that. Here's an example: say we would like to know how much mail a person is going to get every day. If we measure how much mail you get over a time period, and then put that data into the distribution equation, we can predict how likely it is that you'll get three, four, five, or 80 messages on any given day in the future.
People have used this to predict the outcome of sports games or if random farms in Kansas will get hit by a space particle. We aren't too sure why that last one matters, but we have a pretty good guess.
Fibonacci sequence
Probably one of the most famous set of numbers in the world, the Fibonacci sequence can be described by an equation. To find the next number in the sequence, add up the previous two, and presto. The sequence keeps going. It's pretty straightforward but probably holds the keys to the universe.
We can use the Fibonacci Sequence to draw spirals and shapes, which show up in a whole lot of places (some random spirals are falsely described as Fibonacci spirals, but there are also an amazing number of real ones out there). Flowers follow the Fibonacci Sequence. Big things do too: the shape of spiral galaxies follow the Fibonacci sequence, as do the shapes of tropical storms and hurricanes. Why does it show up everywhere? Nobody really knows. It seems like the universe just loves this sequence and keeps producing it.
Not content with letting nature have all the fun, humans have used it for their own creation. The band Tool, never ones to shy away from the weird, put the sequence in their song "Lateralus." The syllables of the lines in the first verse follow the Fibonacci sequence. The first line has one syllable, followed by another with one syllable, followed by a line with two, on and on. The same song has the time signatures arranged in the Fibonacci sequence, and when the tracks are arranged in the album according to the Fibonacci sequence, the album flows smoother. We always knew that Tool held the secrets to the universe.
A really weird example of the Fibonacci sequence is in Lars von Trier's Nymphomaniac. The characters love this sequence, even using it as a guide to how many thrusts they make during sex. It really does show up everywhere!
Tupper's self-referential equation
Remember when that one kid in fifth grade spelled "boobs" with a calculator, and everybody thought he or she was the coolest kid ever? This equation is the grown up version of that.
The Tupper self-referential equation looks like an absolute mess, but when run through a computer, it makes a very specific graph. Graphed equations can look like all sorts of things. Here's one that's a straight line, and here's a curve. When you plot Tupper's self-referential equation, the lines on the graph spell out the equation itself. If that's not mathematical sorcery, we don't know what is.
The same principle can plot a person's name, other equations, or to relive fifth grade shenanigans of spelling out "boobs." Using the technique that Tupper used, people have set up websites to let us spell out words with math.
We have a soft spot for this equation. It doesn't have any profound meaning, or unlock the deep secrets of the universe, it's just a mathematical party trick, something cool for math professors to show off to each other in their down time. If only they had showed us goofy things like this during class, we would have maybe paid attention to the more useful stuff.
BBP algorithm
Quick, what's the 12,094,854,921th digit of pi? Don't know it? Don't worry, we don't either. Picking out random digits of pi is an impossible task. The damn number goes on forever. Fortunately for the human race, a team of mathematicians came up with the BBP algorithm, an equation to find pi's random digits.
That property was totally accidental. The team first developed their equation simply to calculate pi more accurately but then realized they had a digit-extraction algorithm. That's fancy math talk for an algorithm that lets mathematicians figure out the value of a certain digit of a long number without having to calculate the earlier digits.
To use an easier example than that crazy number above, say we wanted to know the 100th digit of pi. Instead of having to memorize all the way up to that digit, we can just use the BBP algorithm to give us the number. We don't even need to know the 99th digit or the 101st digit. That's a pretty amazing thing for an equation to do, especially since it came up accidentally. It does spit out the number in base 16 hexadecimal notation (that's not just a character from the '90s show Reboot, it's a whole different number system), so we have to convert it to our normal base 10 number system. Unless you count in base 16, for some reason.
Riemann zeta function
In school, we all learned about prime numbers. They're numbers that can only be divided by themselves or one. Some examples are 2, 3, 5, 7, and so on. Mathematicians go nuts over them. Specifically, they spend a lot of time trying to predict exactly where the prime numbers occur on the number line. They seem random, but equations like the Riemann zeta function might predict where we can find them.
We aren't going to go too much into the nitty-gritty on the equation, but it has a really weird property. If you graph the function, all the places where the line hits zero can be connected by another line, one related to complex numbers. So what, you might say. That doesn't seem very exciting.
Well, this property, called the Riemann conjecture, influences nearly everything. Researchers see it pop up randomly in quantum mechanics, number theory, and most importantly, figuring out where prime numbers will appear on the number line. And yet the equation remains unproven. Sure, researchers can find proofs for specific solutions (there have already been 10,000,000,000,000 discovered so far), but nobody can find a general proof that works every time. It's such a big problem that mathematicians can win $1 million to solve it.
Before we break out our calculators, it's worth noting that this is one of the most complicated problems of all time. Remember in the movie A Beautiful Mind how Josh Nash (played by Russell Crowe) went crazy? This was the equation that led the real-life Josh Nash into a descent into madness. So enter at your own risk.
Beauty equations
For most of us, finding out how beautiful we are relies on other people's opinion, like how many matches we get on Tinder. But what if we could use mathematics to find out how hot we are? That would be pretty amazing and would make Tinder a much less depressing experience.
One of the best ways to predict the beauty of a person is using the Golden Ratio equation. The Ratio shows up all over nature, including in human faces. If a person's face matches the Golden Ratio more perfectly, then we like that person's face more. It's even possible to change pictures of faces to fit the Golden Ratio and make them even more beautiful. The Ratio holds the key to beauty.
Or does it? Sure, having a really symmetrical face is nice, but what about variation? People's faces are beautiful for different reasons, and if everybody fit the Golden Ratio, the human race would be kind of boring. A whole race of Tom Cruises isn't that interesting.
An MIT team made a better model for beauty and developed an equation that accounted for variations by focusing on the contour and shape of the face on its own, not just relying on a ratio. It uses some complex vector mathematics, and if it works, will allow a computer to predict the beauty of a human face with more accuracy than the Golden Ratio. As for whether it's a good idea to start classifying attractiveness by mathematics, that's a discussion for philosophers.
Schrödinger equation
Most people have heard of Schrödinger's cat, but for people who don't study physics, there really isn't much point in looking at the Schrödinger equation that spawned it. That's too bad, because this relatively straightforward equation holds some of the most tantalizing mysteries of our universe.
The Schrödinger equation describes how quantum systems (like an electron or other particle) evolve over time. It totally revolutionized physics as we know. As people started messing around with it, they noticed that it had some pretty strange properties.
The Schrödinger equation predicts something called quantum tunneling. This effect says that particles can do weird things, if they try to do it long enough. For example, a particle that couldn't travel through a solid wall would be able to, as long as it smashed itself against the wall long enough. In our world of large things, that means if you kept running into an indestructible wall for an infinite amount of time, at some point, all of your particles would just jump through the wall. Fortunately, to do that would take longer than the age of the universe. That sounds absurd, but it's how the Sun works.
The equation also tells us that there are probably parallel universes hanging around. Every time a quantum event occurs, it creates another universe that keeps going on its merry way like nothing happened. So all around us, there are countless parallel universes popping into existence like that Jared Leto movie Mr. Nobody. There could be trillions of copies of us existing in alternate realities. Or so Schrödinger said.
Cantor's proof
Cantor's Proof is one of the mind-blowing ideas in mathematics and it totally reinvented how we think of infinity.
Here's a seemingly absurd question: how big is infinity? Well ... infinitely big, so that question seems useless to ask. But in hard-core mathematics, it's not a useless question at all. In fact, it's super important. Mathematician Georg Cantor investigated the idea of infinity, trying to figure out just how large infinity was. He developed the diagonal proof, which we won't explain here, but you can watch the video above to learn about it. What's most important is the results. Turns out that infinity has a size, and some infinities have different sizes than others.
That probably seems ridiculous, but it's mathematically sound. Cantor was able to show there were an infinite amount of natural numbers, which are whole numbers like 1,2,3,4, and so on. He also showed there was an infinite amount of real numbers, which included all the decimal numbers between all the numbers. Here's the amazing part: the infinite amount of real numbers is bigger than the infinite amount of natural numbers. So there are different sizes of infinity, just like numbers are different!
When we go see Avengers: Infinity War, we'll have ask which infinity it's referring to. That'll make us popular with our friends.
Euler's identity
Considered by every mathematicians as the most beautiful equation in existence, Euler's identity is positively amazing and gives us some look into the interconnectedness of the whole universe. Rockstar scientist Richard Feynman called it "the most remarkable formula in mathematics."
The identity comes from the Euler's equation, which shows up for most students in undergraduate physics. People don't really think much about it. But when the x in the equation is set to pi, the equation equals zero. If it isn't intuitively obvious how amazing this is, don't worry, we'll explain.
With pi in the equation, it includes five of the most fundamental numbers in the universe: 1, 0, e, i (the imaginary root), and pi. Somehow, all five of those numbers are related to each other deep down in mathematics. The equation also has three of the most useful math operators (plus, times, exponentiation) and the relation =. Somehow, all the building blocks of mathematics ended up in the same equation. Amazing, right?
Using these things, any civilization can build mathematics from the ground up, and it's all here in one little equation. If we were to leave one thing for our ancestors, should an apocalypse hit, it would be this identity, which would give them all the mathematical basis they need to rediscover everything we have. You know what, that would be a really interesting idea for a Mad Max movie. Because that's what they need: mathematics.
P=NP
In computational mathematics, there are two types of problems: P problems and NP problems. P problems are a piece of cake for computers. NP problems are those that are not easy, unless we want to wait around 300 quintillion years to get the solution. NP problems are weird though, because a computer can tell us that the answer to an NP problem is right if we show it a solution, it just can't get there easily on its own.
Seems weird? Well here's an example of an NP problem: a salesman wants to visit 100 cities and still make it back home but only has 10,000 kilometers worth of gasoline. Can he make it to all the cities and back home with that gasoline? Think of all the different combinations of routes the salesman can take between all 100 cities, and its pretty easy to see that it would take a long time to figure out a solution because a computer would have to try every possible path.
But if we gave a computer a path already solved, it could pretty easily figure out if the path worked. Just add up all the kilometers, and if its less than 10,000, bam! ... The salesman can easily come and annoy the residents of all the cities.
So what's the big deal? Well, in math-talk, P=NP says that there are no true NP problems. A computer can theoretically solve any complex problem. If somebody can prove that P=NP, they will make a sweet $1 million ... And completely revolutionize the world.
Theorists believe if somebody can prove that P=NP, they will also discover the key to breaking any encryption. How that works is a little beyond us, so we'll just trust the computer people. Everything, from Gmail accounts to Swiss bank passwords would be open! Anybody who verifies P=NP had better hide, because we bet a lot of governments would want them dead.
Friedmann equations
Russian physicist Alexander Friedmann created these equations in the 1920s to explain how the universe was expanding. They show that the universe should expand. But when the equations came out, it looked like the universe wasn't expanding at all. Einstein freaked out about that and added a new term to the equation called the cosmological constant, a new variable to make the equations say that the universe is static. He didn't like the solution, so he broke the equation. It was one of the few times he screwed up.
Soon after he came up with his "fudge factor," astronomers discovered that the universe is expanding. There waso need for a new variable. But that didn't solve the biggest mystery though: what was making the universe expand?
When astronomers started trying to figure it out, they couldn't see anything that would make the universe get bigger and bigger. Friedmann somehow predicted that the universe has a force that has eluded discovery for nearly a century. Eventually, astronomers just called it dark energy. There's definitely something pushing the universe apart, but even today, nobody can figure out what that something is. It's a gigantic mystery, but the equations say that it has to exist. They show us the future of our universe as dark energy pushes things apart. We'll just have to go the Restaurant at the End of the Universe to see how it all ends.
They also imply that the universe might be shaped like a saddle, so that's ... weird.
Russell's paradox
Imagine a barber who has this sign on his store: "Do you shave yourself? If not, come in and I'll shave you! I shave anyone who does not shave himself, and no one else." Seems straightforward, but here's the question: does the barber shave himself?
If he does shave himself, then he shouldn't shave himself because he only shaves people who don't shave themselves. But then that means he has to shave himself, since the first statement means he doesn't shave himself. But now he is contradicting the first statement. He both shaves himself and doesn't shave himself. It goes on and on until our brains explode and we look like that guy in Scanners.
This isn't just a fun logic trick to play on our friends. The mathematical version of this paradox (which only uses variables and a mathematical object called a "set") is a profound statement, and totally revolutionized set theory. It lead to some far-out theories like Godel's Incompleteness theorem, which says that any mathematical system will have problems that are impossible to solve, and the discovery of different sizes of infinity. So the Russell Paradox kind of broke any chance we have of having a totally complete mathematical theory. Not bad for a barber with weird shaving habits.
Sphere eversion
Topology is the field where mathematicians give a big middle finger to reality and do crazy things that look like witchcraft. The field studies how shapes change as they're twisted and deformed, often in ways that can't happen in real life. For example: sphere eversion, which is turning a sphere inside out without making any tears, folds or creases on its surface.
That's impossible to do or even imagine in real life. How can you turn something inside out without tearing or folding it? With math!
Just watch the video above to see how weird a sphere eversion is. Doing one of these mathematically was impossible to prove for a long time. Now, topology people can do it all the time, especially since computers can crunch the equations for us. Without computers, here is what the equations look like. Click at your own risk. That ain't high school geometry.
If it's really hard to see why anybody would care about this stuff, don't worry, most people have a hard time thinking of applications of topology. The field shows up in really random places, from computer coding to chemistry and into the weird world of string theory, a physics theory to describe all of reality. The cutting edge of a ton of fields use topological techniques and mathematics. So who knows, maybe the sphere eversion will hold the secrets of the universe? We just probably have to travel through a black hole to do it or hang out with Dr. Strange.
Future prediction equation
Lots of mathematics revolve around predicting the future. For example: if we drop a ball from an airplane, how long will it take the hit the ground? But some scientists don't want to stop there and want to predict more complex things. According to a group of neuroscientists at the University of Sussex, they may have found a way to predict incoming disasters, from massive problem like stock market crashes to individual tragedies like brain aneurysms. Turns out, those two situation follow similar mathematical trends, even though they're vastly different.
Their equation relies on the flow of information in complex systems and relies on a similar simulation to phase transitions, like what we see when water turns to ice. According to their equation and computer simulations, by analyzing how information flows, we can predict when a "phase change" of fortune will happen, when normal events suddenly turn into a huge catastrophe.
It's a really complex idea, and the paper is hidden behind a paywall, so we can't get a glimpse at the super-cool future prediction equation. Probably for the better. It could melt our brains. Thinking of the flow of events like the change from water to ice is super odd, but supposedly it works. Mathematicians can use it to predict when a future tragedy will happen and then take steps to prevent it, kind of like the cops in Minority Report. Only in this situation, we'll use mathematics, not creepy psychic people. We think that's an improvement.